Table of Contents

Lindenmayer Systems in MGS

Lindenmayer Systems (or L-systems for short) are generative grammars working as a parallel sequence rewriting. A L-system corresponds to a sequence $l$ of symbols transformed using rules of the form $\alpha \rightarrow \beta$ so that if the sub-sequence $\alpha$ is found in $l$, it is replaced by $\beta$. The rewriting strategy is maximal parallel meaning that rules all together through the sequence disjointly and maximally (i.e., such that there is no untouched subsequence containing a sub-sequence $\alpha$). L-systems are widely used for modeling biological systems and particularly for describing growth processes of plant development.

L-systems are by nature easily specified in MGS. In the following, we present two model of growth of Anabaena Catenula based on L-systems and implemented in MGS.

Anabaena Catenula

Anabaena (http://www.micrographia.com/specbiol/bacteri/bacter/bact0200/anabae03.htm)

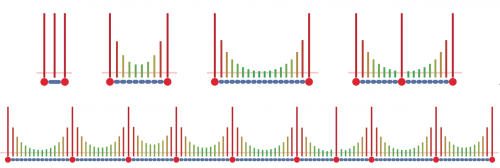
The cyanobacterium Anabaena grows in filaments of 100 cells or more. The growth process exhibits two interesting behaviors:

  • Cell polarities: cells in the filament divide in a asymmetric manner: one of the daughters is longer than the other; more over the two possibilities for ordering the daughters (small-long or long-small) obey to a specific rule.
  • Cell differentiation: when starved for nitrogen, specialized cells called heterocysts differentiate from the photosynthetic vegetative cells at regular intervals along each filament. Heterocysts are anaerobic factories for nitrogen fixation; in them, the nitrogenase enzyme complex is synthesized and the components of the oxygen-evolving photosystem are turned off. Plant signals exert both positive and negative regulatory control on heterocyst differentiation.

Simple Growth Model

Cells in the filament divide in a asymmetric manner: one of the daughters is longer than the other; more over the two possibilities for ordering the daughters (small-long or long-small) obey to a specific rule. A symbolic model of this behavior is described in The Algorithmic Beauty of Plants (pp. 5).

Cell state is symbolically abstracted with two properties:

  • cell size: long or short
  • cell polarity: left or right

Long cells divide quickly than short, and the polarity decide the division ordering (small-long or long-small).

MGS Implementation

Cells have polarities (Left or Right) and two different sizes (Short or Long) 

type cell = `Left_Long | `Right_Long | `Left_Short | `Right_Short ;;

The whole alga is represented by a sequence of cells 

type anabaena = [cell]seq ;;

Let define the initial state S0 as a sequence with a unique long right oriented cell 

S0 :=  seq:(`Right_Long) ;;

Let check that the initial state is of type anabaena (dynamical typing) 

anabaena(S0) ;;

Let define the evolution rules of the cells 

trans grammar = {
 
  // Growth Rules: short cells become long while keeping their polarity
 
  `Right_Short => `Right_Long;
 
  `Left_Short  => `Left_Long;
 
  // Division Rules: long cells divide to give raise to a long cell and a short cell
 
  `Right_Long  => `Left_Long, `Right_Short;
 
  `Left_Long   => `Left_Short, `Right_Long;
 
} ;;

Let apply the evolution rules on the intitial state 

S1 := grammar(S0) ;;
 
S2 := grammar(S1) ;;
 
S3 := grammar(S2) ;;

… which can be written shortly 

S3 := grammar[iter = 3](S0) ;;

Let define a function to get a readable output 

fun output(S) = (
 
  foreach c in S do
    switch c
      case `Right_Short: stdout << "r"
      case `Left_Short:  stdout << "l"
      case `Right_Long:  stdout << "R"
      case `Left_Long:   stdout << "L"
    endswitch;
  stdout << "\n";
  S
 
) ;;

Let output data during the applications 

grammar[iter = 5,
        prelude = output,
        interlude = output,
        postlude = output
       ](S0) ;;

Textual output of the program

Fig. 1.4 of The Algorithmic Beauty of Plants 

R
Lr
lRR
LLrLr
lRlRRlRR
LLrLLrLrLLrLr
lRlRRlRlRRlRRlRlRRlRR
LLrLLrLrLLrLLrLrLLrLrLLrLLrLrLLrLr
lRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRR
LLrLLrLrLLrLLrLrLLrLrLLrLLrLrLLrLLrLrLLrLrLLrLLrLrLLrLrLLrLLrLrLLrLLrLrLLrLrLLrLLrLrLLrLr
lRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRRlRlRRlRlRRlRRlRlRRlRR

The whole code follows

anabaena_growth_model.mgs
type cell = `Left_Long | `Right_Long | `Left_Short | `Right_Short ;;
 
type anabaena = [cell]seq ;;
 
S0 :=  seq:(`Right_Long) ;;
 
anabaena(S0) ;;
 
trans grammar = {
 
  `Right_Short => `Right_Long;
 
  `Left_Short  => `Left_Long;
 
  `Right_Long  => `Left_Long, `Right_Short;
 
  `Left_Long   => `Left_Short, `Right_Long;
 
} ;;
 
fun output(S) = (
 
  foreach c in S do
    switch c
      case `Right_Short: stdout << "r"
      case `Left_Short:  stdout << "l"
      case `Right_Long:  stdout << "R"
      case `Left_Long:   stdout << "L"
    endswitch;
  stdout << "\n";
  S
 
) ;;
 
grammar[iter = 5,
        prelude = output,
        interlude = output,
        postlude = output
       ](S0) ;;

Heterocyst Differentiation Model

(Prusinkiewicz, 2012)

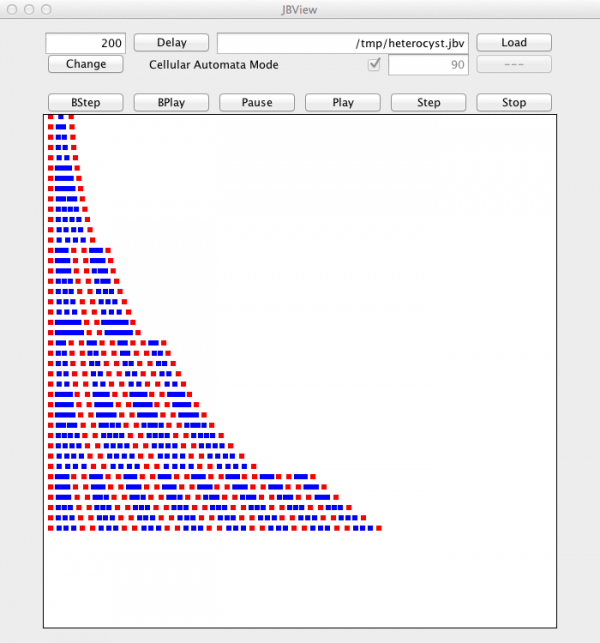
When starved for nitrogen, specialized cells called heterocysts differentiate from the photosynthetic vegetative cells at regular intervals along each filament. Heterocysts are anaerobic factories for nitrogen fixation; in them, the nitrogenase enzyme complex is synthesized and the components of the oxygen-evolving photosystem are turned off. Plant signals exert both positive and negative regulatory control on heterocyst differentiation.

Wilcox et al. have proposed a activator-inhibitor model of heterocysts differentiation where the (high) concentration of the activator triggers the heterocysts differentiation. The production of the activator is an autocatalytic reaction and also catalyzes the production of the inhibitor. The inhibitor is an antagonist substance that repress the activity of the activator when is concentration is high enough. The diffusion of the inhibitor to the neighboring cells prevents neighbors to become also heterocysts and explains why heterocysts appear in a regular spaced pattern in the filament.

The inhibitor have been identified more recently. The inhibition of the differentiation is a protein PatS which is produced by the heterocysts and which diffuses in the neighborbor vegetative cells. The model specified as a parametric L-system is presented in (Prusinkiewicz, 2012)1). The straightforward translation of this model in MGS follows.

MGS Implementation

anabaena_heterocyst_differentiation.mgs
ofile := "heterocyst.jbv" ;;
K     := random(2.0) ;;
v     := 0.5 ;;
R     := 1.1 ;;
T     := 0.1 ;;
Smax  := 0.8 ;;
dt    := 0.001 ;;
 
record W = { J: float } ;;
record C = { a:`V|`H, c:float, s:float, p:`Right|`Left } ;;
record H = C + { a = `H } ;;
type anabaena = [W|C]seq ;;
 
S0 := ({ a = `H, c = 1.0, s = 1.0, p = `Left  }, { J = 0.0 },
       { a = `V, c = 1.0, s = 1.0, p = `Right }, { J = 0.0 },
       { a = `H, c = 1.0, s = 1.0, p = `Left  }) ;;
 
trans rules = {
 
  wall:W => { J = K * (left(wall).c - right(wall).c) } ;
 
  cell:H => cell; 
 
  cell:C =>
    let cell' = cell + { c = cell.c + dt * ((left(cell).J - right(cell).J) - v * cell.c),
                         s = cell.s * (R ** dt) }
    in
      if cell'.c < T
      then cell' + { a = `H, c = 1.0, s = 1.0 }
      elif cell'.s > Smax
      then if cell'.p == `Right
           then (cell' + { s = 3.0 * cell'.s / 4.0, p = `Left  }, { J = 0.0 },
                 cell' + { s = 1.0 * cell'.s / 4.0, p = `Right })
           else (cell' + { s = 1.0 * cell'.s / 4.0, p = `Left  }, { J = 0.0 },
                 cell' + { s = 3.0 * cell'.s / 4.0, p = `Right }) fi
      else cell' + { a = `V } fi
 
} ;;
 
fun output(S) = (
  if iteration % 1000 == 0 then
    fold_indexed((fun p, c, acc ->
                    if C(c)
                    then
                      ofile << " { " << (2.0 * acc + c.s) << " " << (iteration / 500);
                      if c.a == `H then ofile << " 1 0 0 } " else ofile << " 0 0 1 } " fi;
                      acc + c.s
                    else acc fi),
      0.0, S)
  fi;
  S
);;
 
ofile << " { ";;
rules[iter = 40000,
      prelude = output,
      interlude = output,
      postlude = output
     ](S0) ;;
ofile << " }\n" ;;

1) Przemyslaw Prusinkiewicz and Brendan Lane. Modeling Morphogenesis in Multicellular Structures with Cell Complexes and L-systems. In Pattern Formation in Morphogenesis, pp. 137-151, V. Capasso et al. (eds.), Springer, 2013.

Personal Tools