Chemical Modeling
- Stochastic Lotka-Volterra Model
  - MGS Implementation
- Synthetic Multi-cellular Bacterium

Chemical Modeling

Chemical modeling relies on the use of a chemical metaphor to model a system. This kind of system is autonomous and highly parallel. The main idea is to represent data as a (abstract) solution of chemicals and to specify the dynamics using chemical reactions. Chemical modeling has been developed in the context of computer science with the Gamma programming language (Banâtre, Le Metayer, 1986), the CHAM (Chemical Abstract Machine, Berry, Boudol, 1990), or more recently with membrane computing (extension of the chemical metaphor to chemical reactions nested in membranes).

Chemical models are easily expressed in MGS. The adequate topological collection to use is bag/multi-set. The topology associated with this data structure is a complete graph which represents the ability of any value of a bag to interact with any other value: the solution is well mixed. Chemical reactions are then specified as rewriting rules of transformations.

An interesting point lies in the choice of the rule application strategy. Two strategies are particularly used:

the maximal/parallel strategy: it is synchronous and simulates well the fact that reactions may occur in parallel everywhere in the solution,
the Gillespie strategy: this stochastic sequential strategy is based on the Gillespie's SSA¹⁾ which allows simulations where reaction kinetics are respected.

The following examples illustrate the use of the Gillespie strategy.

Stochastic Lotka-Volterra Model

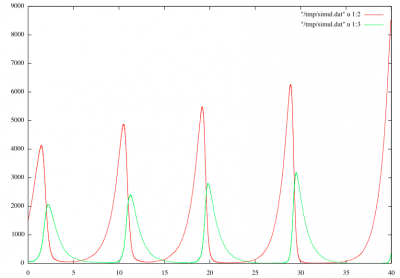A predaor-prey system is composed of two interdependent populations, on of which serves as food source for the other. Such a system exhibits characteristic coupled oscillations. Informally the population dynamics is governed by four simple rules:

Preys spontaneously reproduce
Predators spontaneously die
Predators hunt preys
- Preys may die
- Predators may reproduce (predation efficiency)

The Lotka-Volterra model formalizes this specification with a pair of differential equations:

$\left\{ \begin{array}{lcl} \frac{dV}{dt} & = & V(\alpha - \beta P)\\ \frac{dP}{dt} & = & P(\gamma V - \delta)\\ \end{array}\right.$

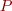where $V$ and $P$ are respectively amounts of preys and predators, and $\alpha$ , $\beta$ , $\gamma$ and $\delta$ are parameters. This system is in fact to mass action law of the following system of chemical reactions

$\left\{ \begin{array}{lcl} V & \stackrel{a}{\longrightarrow} & 2\,V\\ V + P & \stackrel{b}{\longrightarrow} & P\\ V + P & \stackrel{c}{\longrightarrow} & 2\,P\\ P & \stackrel{d}{\longrightarrow} & .\\ \end{array}\right.$

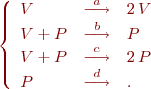
MGS Implementation

Let define some global variables

ofile: name of a file to save simulation data
gnuplot: executable filename of gnuplot

ofile := "/tmp/simul.dat" ;;
gnuplot := "/usr/bin/gnuplot" ;;

Chemicals are of two types: preys and predators

type chemical = `Prey | `Predator ;;

The whole population is represented by a bag (multi-set) of chemicals

type population = [chemical]bag ;;

Let define the initial state S0 as a bag composed of some preys and predators

S0 := 1500 * `Prey + 50 * `Predator ;;

Let check that the initial state is of type population (dynamical typing)

population(S0) ;;

Let define the reaction rules

trans rules = {
 
  // Preys spontaneously reproduce
  `Prey ={ C = 1. }=> `Prey, `Prey;
 
  // Predators spontaneously die
  `Predator ={ C = 1. }=> <undef>;
 
  // Preys eat preys
  `Predator, `Prey ={ C = 0.001 }=> `Predator;
 
  // Predators eat preys and reproduce
  `Predator, `Prey ={ C = 0.001 }=> `Predator, `Predator;
 
} ;;

Let apply the reaction rules on the initial state: the Gillespie strategy (only defined on bags) uses the Gillespie's SSA to trigger a reaction rule

rules[strategy = `gillespie](S0) ;;

Let define a function to save data (ie, for each step, its date, the number of preys, the number of predators)

fun output(S) = (
  if iteration % 10 == 0
  then
    let nb_preys = count(`Prey,S)
    and nb_predators = count(`Predator,S)
    in
      ofile << tau << " " << nb_preys << " " << nb_predators << "\n"
  fi;
  S
) ;;

Let save data during the simulation

rules[strategy = `gillespie,
      prelude = output,
      interlude = output,
      postlude = output,
      iter = 100000
     ](S0) ;;

Let launch gnuplot to visualize

gnuplot << "  plot \"" + ofile + "\" u 1:2 w l\n" ;;
gnuplot << "replot \"" + ofile + "\" u 1:3 w l\n" ;;

prey_predator.mgs

ofile := "/tmp/simul.dat" ;;
gnuplot := "/usr/bin/gnuplot" ;;
 
type chemical = `Prey | `Predator ;;
 
type population = [chemical]bag ;;
 
S0 := 1500 * `Prey + 50 * `Predator ;;
 
trans rules = {
 
  `Prey ={ C = 1. }=> `Prey, `Prey;
 
  `Predator ={ C = 1. }=> <undef>;
 
  `Predator, `Prey ={ C = 0.001 }=> `Predator;
 
  `Predator, `Prey ={ C = 0.001 }=> `Predator, `Predator;
 
} ;;
 
rules[strategy = `gillespie](S0) ;;
 
fun output(S) = (
  if iteration % 10 == 0
  then
    let nb_preys = count(`Prey,S)
    and nb_predators = count(`Predator,S)
    in
      ofile << tau << " " << nb_preys << " " << nb_predators << "\n"
  fi;
  S
) ;;
 
rules[strategy = `gillespie,
      prelude = output,
      interlude = output,
      postlude = output,
      iter = 100000
     ](S0) ;;
 
gnuplot << "  plot \"" + ofile + "\" u 1:2 w l\n" ;;
gnuplot << "replot \"" + ofile + "\" u 1:3 w l\n" ;;

Synthetic Multi-cellular Bacterium

SMB is a iGEM project realized in 2007 by the Paris team. The objective of the SMB project was the design of a synthetic multicellular bacterium. This organism was thought as a tool that would allow the expression of a lethal or dangerous transgenic gene in the Escherichia coli bacterium without disturbing the development of its biomass. MGS have been used to model and simulate the proposed design²⁾.

smb.mgs

(* ********************************************************************************************** *)
(* ********************************************************************************************** *)
(* Global constants                                                                               *)
(* ********************************************************************************************** *)
(* ********************************************************************************************** *)
Na := 6.0221415e23 ;;
VolumeUnit := 1/Na ;;
fun gamma(V) = V ;; // actually Gamma(V)=V*VolumeUnit*Na, but VolumeUnit has been choosen in such a way that Gamma(V)=V waiting for the right volume (mean volume of a germinal bacterium)
 
K_CreD   := 0.2   ;;  // Cre degradation
K_DAPiD  := 0.2   ;;  // DAP degradation
K_DAPApI := 0.5   ;;  // DAPAp inhibition by DAP
K_DAPApA := 0.1   ;;  // DAPAp desinhibition releasing a DAP molecule
K_CreP1  := 1.0   ;;  // Cre production (DAPAp not inhibited)
K_CreP2  := 0.001 ;;  // Cre production (DAPAp inhibited)
K_Diff   := 0.05  ;;  // Differentiation
K_DAPiP  := 1.0   ;;  // DAP production
K_DAPEx  := 0.25   ;;  // DAP export
K_DAPIm  := 0.5   ;;  // DAP import
K_DAPeD  := 0.1   ;;  // DAP degradation
 
K_Div    := 0.02   ;; // Mitosis rate
K_Death  := 0.01   ;; // Death rate
 
fun fstOrder(k,v) = k ;;
fun sndOrder(k,v) = k/gamma(v) ;;
 
appliedBactRule := `Unkown  ;;
DAPEx := 0;
trans inBact[DAPE,v=1] = {
 
  (* Chemicals degradation *)
  `Cre ={ C = fstOrder(K_CreD,1.0)  }=> (appliedBactRule := "CreD"  ; <undef>) ;
  `DAP ={ C = fstOrder(K_DAPiD,1.0) }=> (appliedBactRule := "DAPiD" ; <undef>) ;
 
  (* Promotor activity *)
  `DAPAp, `DAP ={ C = sndOrder(K_DAPApI,1.0) }=> (appliedBactRule := "DAPApI" ; `DAPAp_i) ;
  `DAPAp_i     ={ C = fstOrder(K_DAPApA,1.0) }=> (appliedBactRule := "DAPApA" ; `DAPAp, `DAP) ;
  `DAPAp       ={ C = fstOrder(K_CreP1,1.0)  }=> (appliedBactRule := "CreP1"  ; `DAPAp, `Cre) ;
  `DAPAp_i     ={ C = fstOrder(K_CreP2,1.0)  }=> (appliedBactRule := "CreP2"  ; `DAPAp_i, `Cre) ;
 
  (* Differentiation (exclusively for germinal cells) *)
  `LOXP_Box, `Cre     ={ C = sndOrder(2.0*K_Diff,1.0) }=> (appliedBactRule := "Diff1" ; `LOXP_Box_Cre) ;
  `LOXP_Box_Cre, `Cre ={ C = sndOrder(K_Diff,1.0)     }=> (appliedBactRule := "Diff2" ; `DAP_Box) ;
 
  (* DAP production (exclusively for somatic cells) *)
  `DAP_Box ={ C = fstOrder(K_DAPiP,1.0) }=> (appliedBactRule := "DAPiP" ; `DAP_Box, `DAP) ;
 
  (* DAP externalization & internalization *)
  `DAP   ={ C = fstOrder(K_DAPEx,1.0)                }=> (appliedBactRule := "DAPEx"; DAPEx := DAPEx+v; <undef>) ;
  _ as x ={ A = (\c.(DAPEx * fstOrder(K_DAPIm,1.0))) }=> (appliedBactRule := "DAPIm"; DAPEx := DAPEx-v; x, `DAP) ;
 
} ;;
 
output := "/tmp/smb.dat" ;;
fun SMBoutput[ofile=output](m,c) = (
  if (iteration%m == 0) then (
    stdout << iteration << " " << tau << "\n";
    ofile           <<
    tau             << " " << 
    appliedBactRule << " " << 
    DAPEx           << " " << 
    count(`DAP,c)   << " " << 
    count(`Cre,c)   << "\n"
  ) else 0 fi;
  c
) ;;
 
DAPEx:=1000;
inBact[DAPE=10,
       v=0,
       strategy=`gillespie,
       postlude=SMBoutput(10),
       interlude=SMBoutput(10),
       prelude=SMBoutput(10),
       fixpoint=(\c1.\c2.(tau>=100))
      ](bagify(((#10 `DAP), `DAPAp, `LOXP_Box, seq:())));;
 
system("gnuplot -persist script") ;;

script

set xlabel "Time"
set ylabel "Number of molecules"
set logsc y
plot   [0:100] [100:1300] "/tmp/smb.dat" using 1:3 title 'DAPEx' with lines
replot                    "/tmp/smb.dat" using 1:4 title 'DAP' with lines
replot                    "/tmp/smb.dat" using 1:5 title 'Cre' with lines

¹⁾ Daniel T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys. Chem., 1977, 81 (25), pp 2340–2361

²⁾ Antoine Spicher, Olivier Michel, and Jean-Louis Giavitto, Understanding the dynamics of biological systems, chapter Interaction-based simulations for Integrative Spatial Systems Biology, pages 195-231. Springer, 2011

Chemical Modeling

Stochastic Lotka-Volterra Model

MGS Implementation

Synthetic Multi-cellular Bacterium

Views

Navigation

Personal Tools

Search